10 Time Travel Theories in Physics

When Albert Einstein published his 1905 paper on special relativity he showed something startling yet testable: moving clocks run slow. That simple result helped turn time from an immutable backdrop into a physical quantity that depends on motion and gravity. A few decades later general relativity (1915) completed the picture by making spacetime itself dynamical, and the consequences reach from GPS satellites down to thought experiments about looping histories.

Physicists still argue about whether equations that permit closed loops in time correspond to realizable machines or merely mathematical curiosities. The debate matters: engineers correct GPS clocks by roughly 38 microseconds per day to account for relativistic effects, philosophers worry about causality, and writers borrow the math for popular stories. This survey of time travel theories in physics presents ten influential ideas — from everyday time dilation to exotic wormholes, quantum models, and proposed safeguards such as chronology protection — and evaluates their plausibility, experimental touchpoints, and the conceptual problems they raise.

Foundations and Classical Relativity

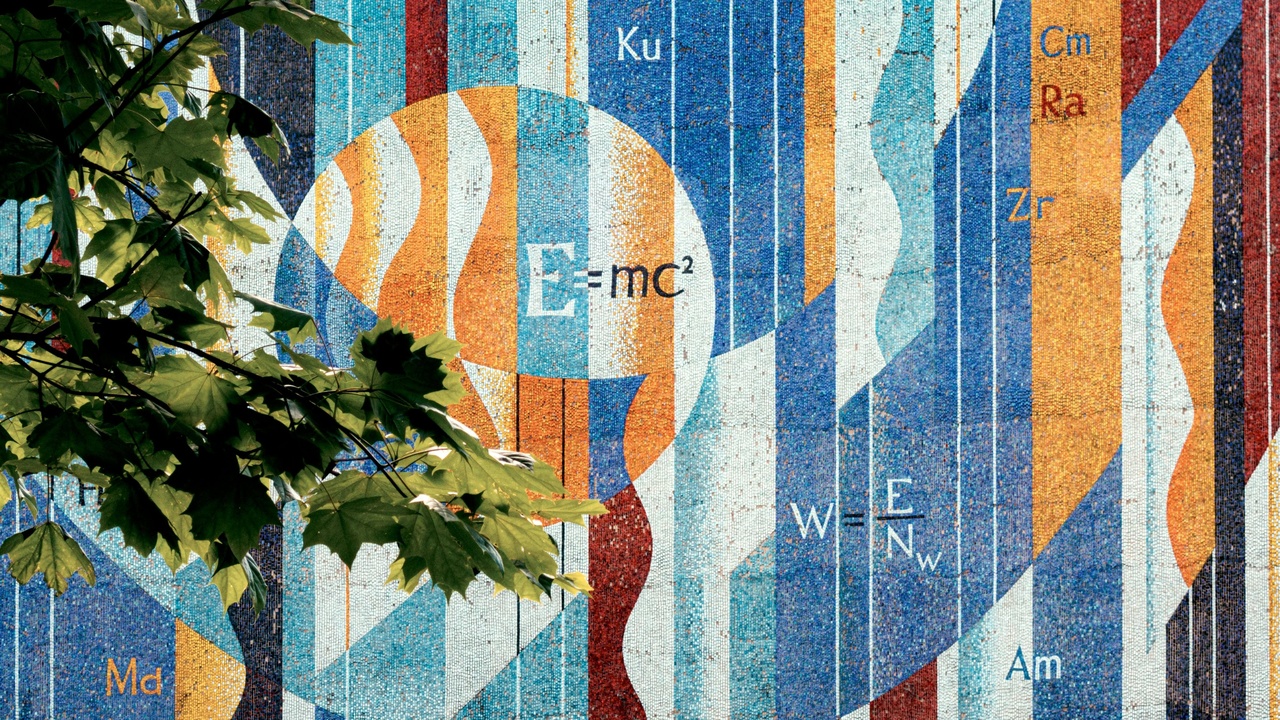
Special relativity (Einstein 1905) and general relativity (Einstein 1915) rewired how physicists think about time. In special relativity simultaneity is frame-dependent and moving clocks tick differently from stationary ones. General relativity goes further, tying clock rates to gravitational potential through spacetime curvature. Both theories have concrete, repeatable consequences: the Hafele–Keating airplane-clock flights in 1971 confirmed relativistic clock shifts, and GPS platforms require combined special- and general-relativistic adjustments of about 38 microseconds per day to stay synchronized.

Mathematically, Einstein’s field equations admit a wide variety of exact solutions, some of which contain closed timelike curves (CTCs) — worldlines that return to their own past. Whether such solutions represent physically attainable spacetimes depends on energy conditions, global topology, and back-reaction from quantum fields. The next four entries are classical-relativity avenues that people often label “time travel,” along with the practical and observational limits on each.

1. Time Dilation (Special Relativity)

Special relativity straightforwardly predicts time dilation: a clock moving relative to an observer ticks slower. Einstein derived the relation in 1905, and experiments have repeatedly confirmed it. The Hafele–Keating experiment (1971) flew atomic clocks around the world and measured the expected offsets when compared with reference clocks on the ground.

Time dilation isn’t a science-fiction time machine; it’s an operational adjustment. GPS system engineers apply a special-relativity correction of about +7 microseconds/day and a general-relativity component so the net correction is roughly +38 microseconds/day. High-energy physics gives another vivid example: muons created by cosmic rays live longer in the lab frame because their internal clocks slow relative to Earth, allowing many to reach the surface.

2. Gravitational Time Dilation and Closed Timelike Curves (General Relativity)

General relativity predicts gravitational time dilation: clocks deeper in a gravity well run slower than those farther away. Some exact GR solutions go further and permit closed timelike curves, meaning an object could follow a timelike path and return to an earlier event on its own worldline.

A prominent example is the Kerr metric for a rotating black hole. In certain regions inside the Kerr solution the causal structure is exotic and mathematically allows loops in time, though event horizons and singularities complicate any operational scheme. Other solutions, like the van Stockum and Tipler-like rotating matter distributions, also admit CTCs under special conditions. Observationally, LIGO’s detections of black-hole mergers since 2015 confirm rotating black holes exist, but the extreme mass, spin, and horizon structure make using such objects as time machines effectively impossible.

3. Wormholes (Einstein–Rosen Bridges)

Wormholes are theoretical tunnels connecting distant regions of spacetime, a concept that traces back to Einstein and Rosen in 1935. A traversable wormhole could, in principle, function as a shortcut between two events.

Morris and Thorne’s 1988 analysis showed that if two wormhole mouths undergo different relativistic histories — for example, one is accelerated or placed in a stronger gravitational potential — a time offset builds between them. Passing through the wormhole could then move you to the other mouth’s earlier proper time, creating an effective time loop. The catch: traversable wormholes require exotic matter that violates known energy conditions. Real negative-energy effects like the Casimir force are real but tiny, far short of the amounts semiclassical estimates suggest are needed for macroscopic, stable wormholes.

4. Tipler Cylinder and Rotating-Universe Solutions (Gödel Metric)

Some exact solutions of Einstein’s equations allow CTCs through global structure rather than localized tunnels. Kurt Gödel’s rotating-universe solution from 1949 is a famous cosmological example where the entire spacetime has closed timelike curves. Frank Tipler later proposed that an infinitely long, extremely dense rotating cylinder could produce CTCs in its exterior region.

These constructions are primarily theoretical counterexamples that expose how global topology and rotation affect causality. Physically they require unrealistic assumptions — infinite length, enormous mass densities, or a global rotating cosmology inconsistent with observations. They’re useful for thought experiments but not blueprints for engineering backwards trips.

Quantum and Microscopic Approaches

Quantum mechanics reshapes causal intuition at microscopic scales and suggests alternative ways to think about time. Everett’s relative-state formulation (1957) reframed quantum measurement as branching histories. Later quantum-information proposals — Deutsch’s quantum model for CTCs (1991) and post-selected teleportation variants — recast closed timelike behavior in density-matrix or post-selection language.

Any naive extrapolation must respect the Planck scale (length ≈ 1×10‑35 meters), where classical spacetime notions likely break down. Some laboratory experiments in quantum optics emulate aspects of post-selection and fixed-point behavior, but these are simulations rather than demonstrations of macroscopic causality violation. The next three items summarize leading quantum and quantum-gravity flavored ideas and their limits.

5. Many-Worlds Interpretation and Branching Timelines

The Everett or Many-Worlds interpretation (1957) sidesteps classical paradoxes by proposing that all measurement outcomes occur in different branches of a universal wavefunction. Under this view, an action that would create a grandfather paradox instead produces a different branch where the paradoxical outcome occurs without contradiction.

This is primarily an interpretational strategy rather than an engineering route to time travel. It resolves inconsistency by multiplying histories rather than changing a single past, and it’s been used in computational toy models to illustrate how paradoxes map to branching structures. Many-Worlds changes how we think about information flow, but it doesn’t provide a mechanism to physically transport macroscopic objects to earlier branches.

6. Deutsch CTCs and Post-Selected Time Loops

David Deutsch proposed a model in 1991 that formulates CTCs in quantum-information terms. The idea is to demand a fixed-point density matrix on the loop: the state entering a CTC must equal the state that emerges after interacting with its past self. This self-consistency at the quantum level can avoid paradoxes while allowing nonclassical correlations.

Variants based on post-selected teleportation (advocated by Seth Lloyd and others) show that post-selection and certain quantum circuits can emulate aspects of time-loop behavior and even suggest computational speedups for specific problems. Experimental quantum-optics setups can simulate post-selection circuits, but these simulations don’t imply macroscopic time travel and sometimes clash with thermodynamic or no-signaling principles when pushed beyond carefully constrained models.

7. Quantum Gravity Hints: Loop Quantum Gravity and String-Theory Speculations

A complete theory of quantum gravity is the natural arena to decide whether classical time-loop solutions survive at the Planck scale. Loop quantum gravity suggests spacetime has discrete structure that could remove classical singularities, while string theory introduces extra dimensions and richer topologies that change causal possibilities.

Both approaches are suggestive rather than conclusive. Quantum-gravity effects might eliminate regions that classically admit CTCs, or they might permit exotic topologies in regimes we can’t probe. So far there’s no experimental confirmation; the Planck length (~1×10‑35 m) remains many orders of magnitude below current collider reach, which keeps conclusions speculative.

Paradoxes, Constraints, and Experimental Tests

Even when the mathematics permits time loops, logical consistency and experimental data impose strong constraints. Philosophers and physicists developed self-consistency principles and conjectures to block paradoxical solutions. At the same time, precision experiments — atomic clocks, GPS, particle timing, and astrophysical observations — provide concrete limits on exotic causal behavior. The following three entries describe prominent consistency proposals and the experimental record that bounds them.

8. Novikov Self-Consistency Principle

Igor Novikov and collaborators in the 1980s articulated the self-consistency principle: if CTCs exist, only those events that are globally self-consistent can occur. In other words, local actions on a time loop must match a history that remains contradiction-free.

Applied to the grandfather paradox, Novikov’s rule forbids any sequence of actions that would prevent the time traveler’s existence; instead, initial conditions conspire so the traveler’s past is unchanged. In model systems this principle often appears as a fixed-point condition for classical or quantum states. The implication is stark: free initial data are restricted by global consistency, which raises philosophical questions about determinism and agency on spacetimes that admit CTCs.

9. Hawking’s Chronology Protection Conjecture

Stephen Hawking proposed his chronology protection conjecture in 1992: the laws of physics prevent macroscopic time machines from forming. The heuristic argument is that vacuum fluctuations and quantum fields near a would-be CTC amplify and produce large stress-energy that back-reacts on spacetime, destroying the causal pathology before it becomes operational.

Semiclassical calculations lend some support — divergences appear in many model computations — but they are inconclusive because a full quantum-gravity treatment is required. Many physicists find the conjecture plausible as a global safeguard, but it remains an idea rather than a theorem until the high-energy behavior of spacetime is fully understood.

10. Experimental Constraints, False Alarms, and Practical Limits

Precision experiments both confirm relativity and limit exotic claims. The Hafele–Keating flights (1971) verified relativistic clock shifts, and GPS’s net correction of roughly +38 microseconds per day is a daily technological reminder that relativistic time effects are real and measurable. No laboratory experiment has produced macroscopic causality violation.

History also offers cautionary tales. The OPERA neutrino anomaly in 2011 suggested faster-than-light travel, but the effect traced to a faulty timing fiber and a miscalibrated oscillator. High-energy experiments and astrophysical timing — from pulsar arrivals to neutrino time-of-flight measurements — place stringent bounds on departures from standard causal structure. In short, extraordinary instrument checks and cross-validation are essential when an observation would challenge causality.

Summary

• Relativity already gives genuine time-manipulation effects used in technology: moving and low-orbit clocks require corrections (GPS net ≈+38 microseconds/day) and experiments such as Hafele–Keating (1971) and muon lifetime measurements demonstrate time dilation.
• Classical general relativity admits mathematical time-loop solutions — Kerr black holes, wormholes (Einstein–Rosen bridges), Gödel cosmologies, and Tipler cylinders — but they rely on extreme, often unrealistic assumptions like infinite cylinders, near-extremal spins, or exotic matter.
• Quantum proposals (Many-Worlds branching, Deutsch’s quantum CTCs, and post-selected teleportation) reframe paradoxes and suggest novel information-theoretic behavior, yet they remain interpretational or simulated in the lab rather than producing macroscopic backward causation.
• Consistency principles and experimental constraints matter: Novikov-style fixed points, Hawking’s chronology protection conjecture (1992), and precision timing tests together make operational time machines highly implausible with current physics.
• Research in quantum gravity and ever-more-precise clocks will sharpen the picture; follow developments in quantum-gravity theory and timing experiments to see whether any classical loopholes survive the Planck-scale verdict.